学生管理系统
计算机组成原理
缓存
microsoft
费用流
random
python考级
springboot
kudu读写流程
ROBOGUIDE
系统错误
pyqt
debian
EEG
pytest
hibernate
coinbase
质量管理
clipStudioPaint
fastapi
傅里叶变换
2024/4/13 11:10:56理解离散傅立叶变换(三.复数)
原文链接 https://blog.csdn.net/dznlong/article/details/2275540 理解离散傅立叶变换(三)------复数形式离散傅立叶变换复数形式的离散傅立叶变换非常巧妙地运用了复数的方法,使得傅立叶变换变换更加自然和简洁,它并不是只是简单…
傅里叶变换之掐死教程
转自知乎详细图片也可参考知乎https://zhuanlan.zhihu.com/p/19759362?fromtimeline&isappinstalled0 我保证这篇文章和你以前看过的所有文章都不同,这是12年还在果壳的时候写的,但是当时没有来得及写完就出国了……于是拖了两年,嗯&…
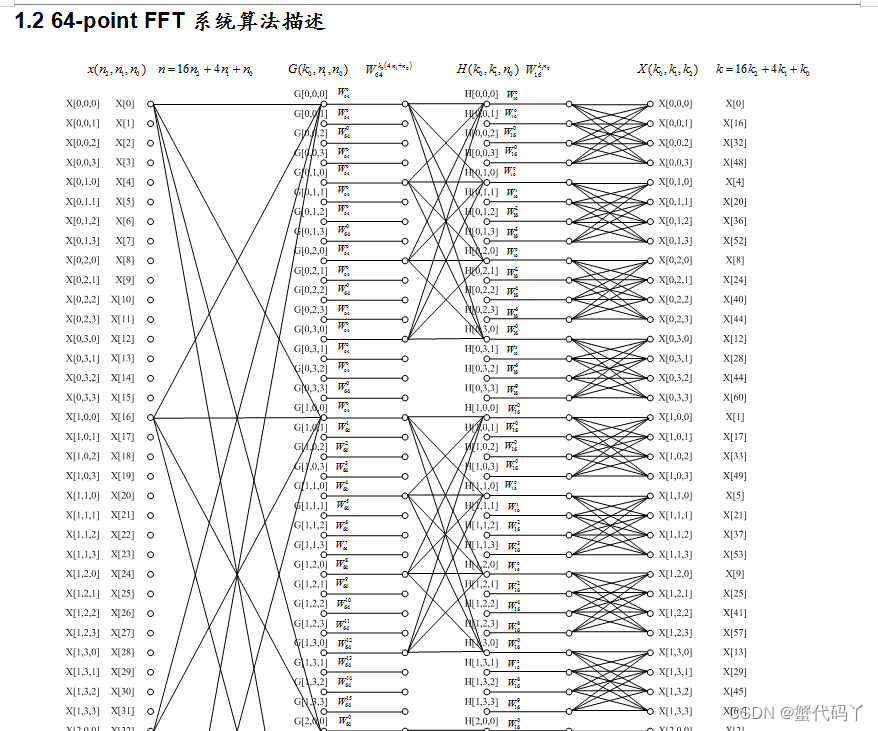
FPGA的64点FFT代码及报告,verilog快速傅里叶变换
名称:64点FFT快速傅里叶变换Radix4
软件:Quartus
语言:Verilog
代码功能: 使用verilog实现64-point Pipeline FFT处理器
FPGA代码资源下载网:hdlcode.com
代码下载:
名称:64点FFT快速傅里…
[EE261学习笔记] 3+.傅里叶变换的三个实例:矩形函数、三角函数与高斯函数
矩形函数: Π(t){1,∣t∣<120,∣t∣≥12\Pi(t) \begin{cases} 1, &\left\lvert t \right\rvert<\frac{1}{2}\\ 0, &\left\lvert t \right\rvert\geq\frac{1}{2} \end{cases}Π(t){1,0,∣t∣<21∣t∣≥21 对其进行傅里叶变换,我…
[EE261学习笔记] 4.常用的几个傅里叶变换相关公式
在本文开始前,需要说明一点,以下推导出的各项公式,只是为了实际计算中方便,并不都有其对应的物理意义。 首先,我们写出符号 f−(t)f(−t)f^-(t) f(-t)f−(t)f(−t),显然,对于奇函数而言&#x…
理解离散傅立叶变换(四. 复数形式离散傅立叶变换)
原文链接 https://blog.csdn.net/dznlong/article/details/2280867 理解离散傅立叶变换(四)------复数形式离散傅立叶变换复数形式的离散傅立叶变换非常巧妙地运用了复数的方法,使得傅立叶变换变换更加自然和简洁,它并不是只是简单…
傅里叶变换、拉普拉斯变换、Z 变换的联系是什么?为什么要进行这些变换?
原创 逸珺 嵌入式客栈
[导读] 在知乎上看到一个问题,傅里叶变换、拉普拉斯变换、Z 变换的联系是什么?为什么要进行这些变换?我觉得这是一个非常好的问题,貌似一下子也回答不上来,所以整理学习并分享一下。 什么是数学…
Fourier分析入门——第11章——Fourier变换
目录 第11章 Fourier变换(Transform)
11.1 引言
11.2 逆向正弦和余弦变换(The Inverse Cosine and Sine Transforms)
11.3 正向正弦和余弦变换(The Forward Cosine and Sine Transforms)
11.4 离散谱对比谱密度(Discret spectra vs. spectral density)
11.5 Fourier变换的…
理解离散傅立叶变换(二. 实数形式离散傅立叶变换)
转载原文链接 https://blog.csdn.net/dznlong/article/details/2269827 理解离散傅立叶变换(二)------实数形式离散傅立叶变换(Real DFT)上一节我们看到了一个实数形式离散傅立叶变换的例子,通过这个例子能够让我们先对…
从信号处理角度彻底理解FFT
只想速览公式可以转到简明FFT公式 一、FFT起初用于解决的问题
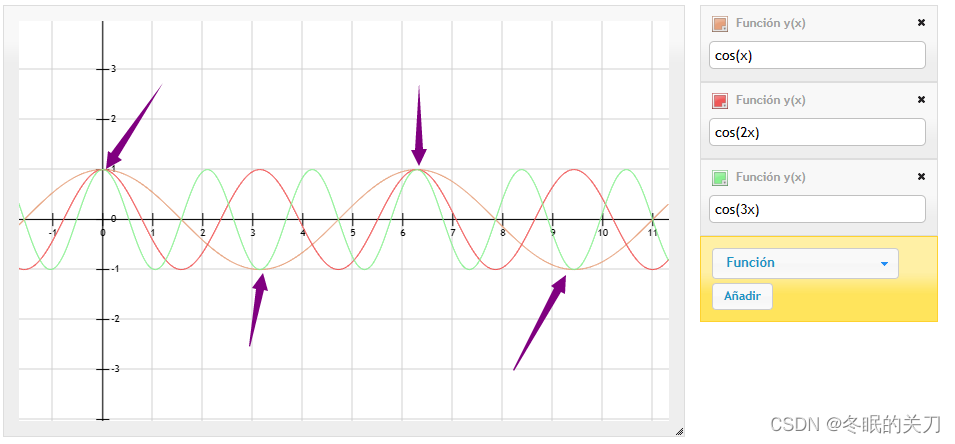
分解复合信号 将复合信号视为若干正弦波与余弦波的叠加,如何得知某个正弦波/余弦波在该信号中的强度?
二、即答
用特定频率的正弦波/余弦波(设其为a)乘上复合信号…
FFT64点傅里叶变换verilog蝶形运算,代码和视频
名称:FFT64点verilog傅里叶变换
软件:Quartus
语言:Verilog
代码功能: 使用verilog代码实现64点FFT变换,使用蝶形运算实现傅里叶变换
演示视频:http://www.hdlcode.com/index.php?mhome&cView&…
傅里叶变换FT与STFT简介
文章目录1 傅里叶变换FT2 短时傅里叶变换STFT如果信号的幅度和频率内容都不会随着时间的变化而变化,则称此信号是平稳的信号,如频率内容不变的正弦波。
如果信号的幅度随时间变化或信号的频率内容随时间变化,称此信号是非平稳信号。
1 傅里…
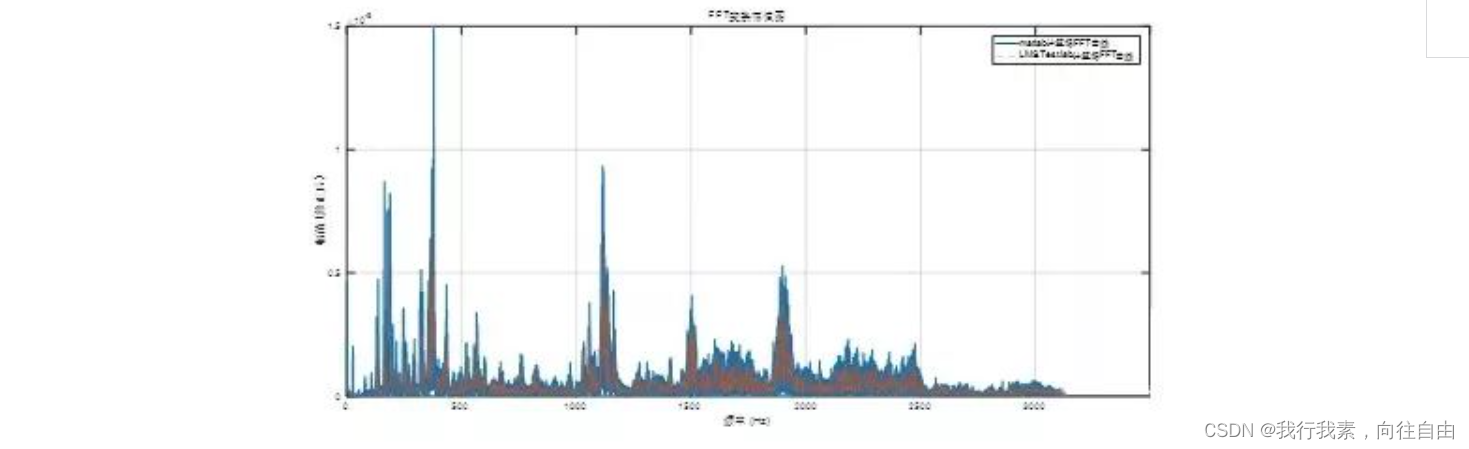
快速傅里叶变换FFT在MATLAB中的实现
一、FFT的由来
首先,为什么要进行傅里叶变换?将时域的信号变换到频域的正弦信号,正弦比原信号更简单,且正弦函数很早就被充分地研究,处理正弦信号比处理原信号更简单。正弦信号的频率保持性:输入为正弦信号…
基于傅里叶变换的运动模糊图像恢复算法matlab仿真
目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
4.1、傅里叶变换与图像恢复
4.2、基于傅里叶变换的运动模糊图像恢复算法原理
5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本
matlab2022a
3.部分核心程序
%获取角度
img…
脑电时频分析I:谱分析
1、EEG频带划分
自发的EEG活动在活体大脑中持续存在,通常通过频率进行分类(也叫神经振荡活动)特定频段的脑活动,即节律性的活动,具有特定的头皮分布和生物学意义 最后还有一个γ波,主要是指30hz~100hz的…
【数字图像处理】图像的数学变换之傅里叶变换
傅里叶变换是分析线性系统的一个有力工具。 从数学意义上说,傅里叶变换将一个任意的周期函数分解成为无穷个正弦函数的和的形式;从物理效果上看,傅里叶变换实现了将信号从空间域到频率域的转换。关于傅里叶变化的讲解,很多大神都…
Fourier变换中的能量积分及其详细证明过程
Fourier变换中的能量积分及其详细证明过程
在使用Fourier变换分析信号时候,有时需要用到能量积分。本文对Fourier变换的能量积分进行分析。
一、Fourier变换中的能量积分
若 F ( ω ) F [ f ( t ) ] F(\omega)\mathscr F[f(t)] F(ω)F[f(t)],则有 ∫…
通过傅里叶变换进行音频变声变调
文章目录 常见音频变声算法使用Wav库读写音频文件使用pitchShift算法进行音频变调主文件完整代码工程下载地址常见音频变声算法
在游戏或者一些特殊场景下为了提高娱乐性或者保护声音的特征,我们会对音频进行变声变调处理。常用的算法包括: 1.基于傅里叶变换的频域算法,该类…
C++版本的OpenCV实现二维图像的卷积定理(通过傅里叶变换实现二维图像的卷积过程,附代码!!)
C版本的OpenCV库实现二维图像的卷积定理过程详解 前言一、卷积定理简单介绍二、不同卷积过程对应的傅里叶变换过程1、“Same”卷积2、“Full”卷积3、“Valid”卷积 三、基于OpenCV库实现的二维图像卷积定理四、基于FFTW库实现的二维图像卷积定理五、总结与讨论 前言
工作中用…
万物皆可傅里叶|傅里叶分析之掐死教程(完整版)
这篇文章的核心思想就是:要让读者在不看任何数学公式的情况下理解傅里叶分析。
更多精彩请关注微信公众号:医械测试~ 傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。 但不幸的是,傅里叶分析的…
机器学习实践系列之14 - OpenCV之傅里叶变换
关于 傅里叶变换,讲的太多了,这里我就不再啰嗦一遍了,原理的东西大家可以搜一下,推荐一篇文章: 如果看了此文你还不懂傅里叶变换,那就过来掐死我吧 这篇文章写得很不错了,从 频域 到傅里叶级数 …
信号处理之快速傅里叶变换(FFT)
信号处理之快速傅里叶变换FFT 历史溯源欧拉公式傅里叶级数(FS)傅里叶变换(FT)离散傅里叶级数(DFS)离散时间傅里叶变换(DTFT)离散傅里叶变换(DFT)快速傅里叶变换(FFT)MATLAB中常用的FFT工具FFT中常见的问题 历史溯源
相信很多人知道傅里叶变换,但是很多人对傅里叶变…
数字图像处理 使用C#进行图像处理九 实现傅里叶变换
一、简述 傅立叶变换将图像分解为其正弦和余弦分量。换句话说,它将图像从空间域变换到频率域。这个想法是任何函数都可以用无限正弦函数和余弦函数之和来精确近似。傅里叶变换是实现此目的的一种方法。 网上有很多关于傅里叶变换的文章,这里就不进行赘述了,这里主要结合代码…
信号与线性系统翻转课堂笔记9——傅里叶变换
信号与线性系统翻转课堂笔记9——傅里叶变换
The Flipped Classroom9 of Signals and Linear Systems
对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著
一、要点
(1,重点)…
Fourier变换的乘积定理及其详细证明过程
Fourier变换的乘积定理及其证明过程
Fourier变换的乘积定理是进行有关Fourier相关运算的有力工具。借助它,可以让有的频域乘积计算或时间域计算有效转化,避开复杂的基于定义的计算过程,使得计算过程快捷方便,本博文在此ÿ…
信号与线性系统翻转课堂笔记9——傅里叶变换概念
信号与线性系统翻转课堂笔记9——傅里叶变换
The Flipped Classroom9 of Signals and Linear Systems
对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著
一、要点
(1,重点)…
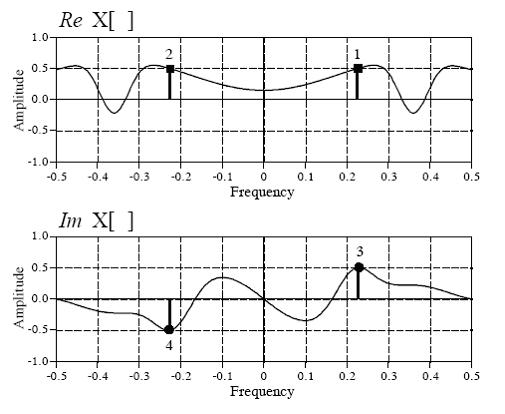
【OFDM系列】DFT为什么能求频率幅度谱?DFT后的X[k]与x(n)幅度的关系?DFT/IDFT底层数学原理?
文章目录 问题引入铺垫一些小公式DFT公式证明DFT公式分解为4部分先考虑k10的情况:再考虑k1≠0的情况: DFT计算后,X(k)与x(n)的关系: Matlab FFT示例代码IDFT公式证明Matlab调用FFT/IFFT并绘图 问题引入 上面是DFT和IDFT的公式,IDFT先不谈。在…
FPGA的256点FFT调用Quartus IP核实现VHDL傅里叶变换
名称:256点FFT调用Quartus IP核实现傅里叶变换
软件:Quartus
语言:VHDL
代码功能:使用VHDL实现256点FFT,调用Quartus IP核实现傅里叶变换
演示视频:http://www.hdlcode.com/index.php?mhome&cView…
频谱功率谱的应用与代码实现
1. 背景:
早前接手一个小项目,使用振动传感器监测风机的开关。
这里不对单片机的使用和加速度传感器的数据采集多做说明。
数据准备:振动采样频率设置为400Hz。采样点为512个点。
由离散点FFT可知,实际可以监测的频率范围&…
【经验模态分解】4.信号由时域向频域的转换
/*** poject 经验模态分解及其衍生算法的研究及其在语音信号处理中的应用* file 傅里叶变换与小波变换* author jUicE_g2R(qq:3406291309)* * language MATLAB* EDA Base on matlabR2022b* editor Obsidian(黑曜石笔记软件&#…
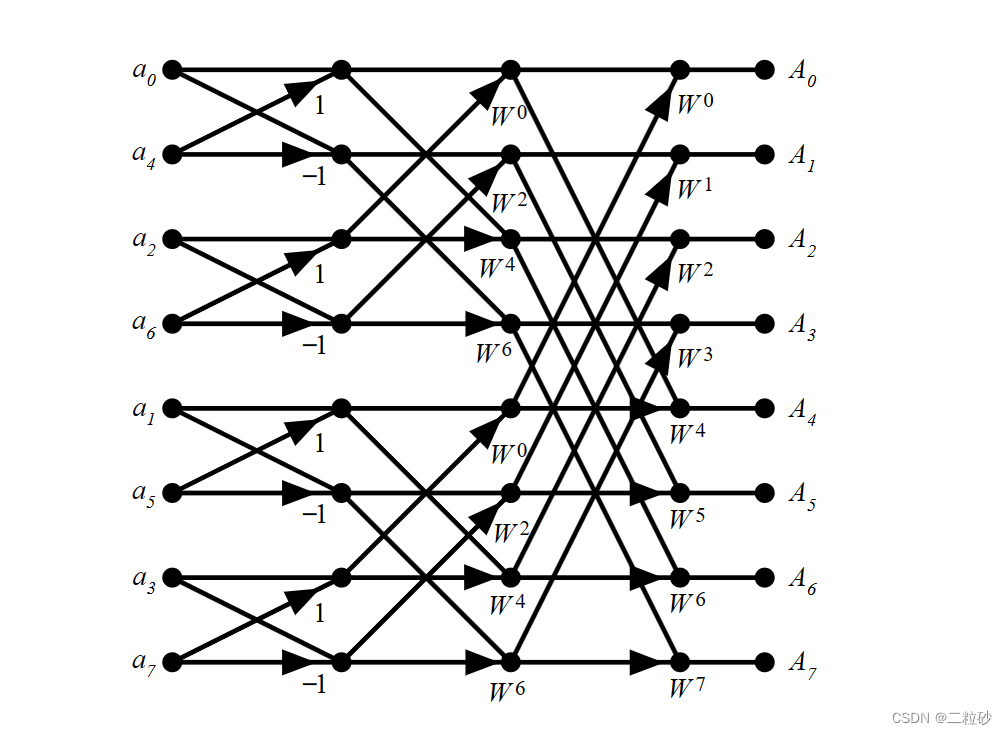
【FFT】快速傅里叶变换
开个新坑, 快速傅里叶变换在现在世界的各个领域都发挥重要作用。 包括音视频压缩、5G、WIFI、卷积、航空、雷达、核武等等
为什么使用快速傅里叶变换
快速傅里叶变换计算复杂度仅为O(nlogn) 而原傅里叶变换是O(n^2)
什么是快速傅里叶变换
是指对傅里叶变换中的重…
【复变函数笔记】傅里叶变换和拉普拉斯变换
文章目录 一、傅里叶变换和拉普拉斯变换的定义1. 傅里叶积分2. 傅里叶变换3. 单位脉冲函数和单位阶跃函数4. 拉普拉斯变换 二、常见函数的傅里叶变换和拉普拉斯变换三、傅里叶变换和拉普拉斯变换的性质 一、傅里叶变换和拉普拉斯变换的定义
1. 傅里叶积分
傅里叶积分定理 若 …
连续Fourier变换及其逆变换的计算表达式
连续Fourier变换及其逆变换的计算表达式
一、关键计算式
若函数 f ( t ) f(t) f(t)满足Fourier积分定理的条件,则在 f ( t ) f(t) f(t)的连续点处, 有 f ( t ) 1 2 π ∫ − ∞ ∞ [ ∫ − ∞ ∞ f ( τ ) e − j ω τ d τ ] e j ω t d ω f(t) \frac{1}{{2{\rm{\pi …
深入浅出的讲解傅里叶变换(真正的通俗易懂)
**
原文地址:https://www.cnblogs.com/h2zZhou/p/8405717.html
转载仅为方便个人学习,并无他意,如有冒犯,敬请谅解 ** <div id"post_detail">深入浅出的讲解傅里叶变换(真正的通俗易懂) …
小波变换 完美通俗解读
申明:小波变换 完美通俗解读,是《小波变换和motion信号处理》系列中的第一篇。原始出处为windstorm的网站http://www.kunli.info/,并非本站原创,但这位大师深入浅出的讲解了小波变换,是你在学习小波的过程中…
傅里叶变换与傅里叶级数理解
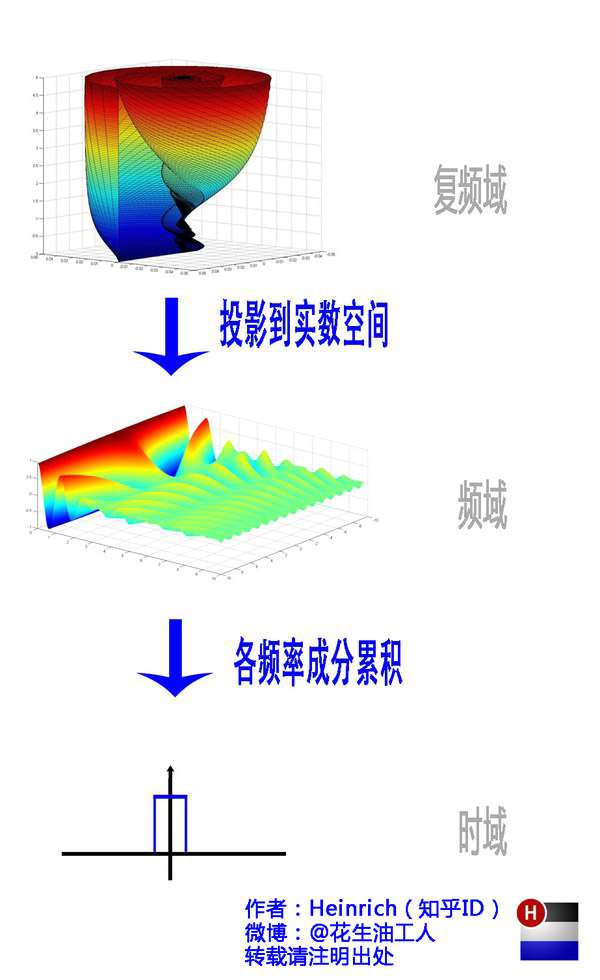
作 者:韩 昊 知 乎:Heinrich 微 博:花生油工人 知乎专栏:与时间无关的故事 谨以此文献给大连海事大学的吴楠老师,柳晓鸣老师,王新年老师以及张晶泊老师。 转载的同学请保留上面这句话,谢谢。如果…
Fourier傅里叶变换的线性性质和位移性质
Fourier傅里叶变换的线性性质和位移性质
为了阐述方便, 假定在这些性质中, 凡是需要求Fourier变换的函数都满足Fourier积分定理中的条件。在证明这些性质时, 不再重述这些条件。
一、线性性质
设 F 1 ( ω ) F [ f 1 ( t ) ] {F_1}(\omega ) {\mathscr F}[{f_1}(t)] F1(…
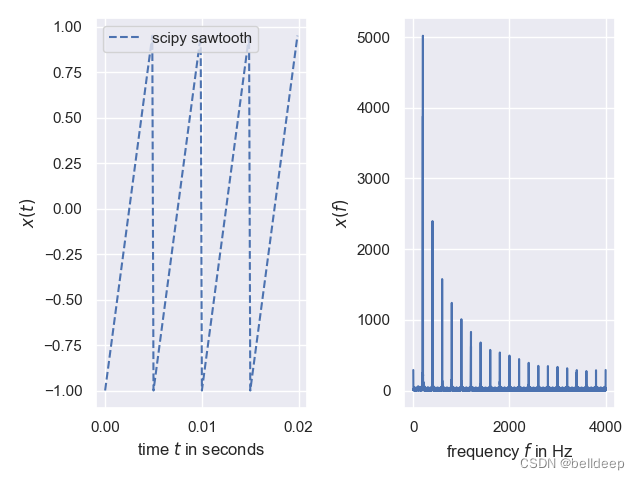
python:傅里叶分析,傅里叶变换 FFT
使用python进行傅里叶分析,傅里叶变换 FFT 的一些关键概念的引入:
1.1.离散傅里叶变换(DFT) 离散傅里叶变换(discrete Fourier transform) 傅里叶分析方法是信号分析的最基本方法,傅里叶变换是傅里叶分析的核心&…
java 使用 jtransforms 傅里叶库通过时域转频域实现wav 音频的加速与变慢效果
引入 maven 依赖:<dependency><groupId>net.sourceforge.jtransforms</groupId><artifactId>jtransforms</artifactId><version>2.4.0</version></dependency> FourierTransformTest.java: import edu.…
Fourier分析导论——第5章——实数据R上的Fourier变换(E.M. Stein R. Shakarchi)
第5章 实数域ℝ上的Fourier变换
The theory of Fourier series and integrals has always
had major difficulties and necessitated a large math-
ematical apparatus in dealing with questions of con-
vergence. It engendered the development of methods
of summa…
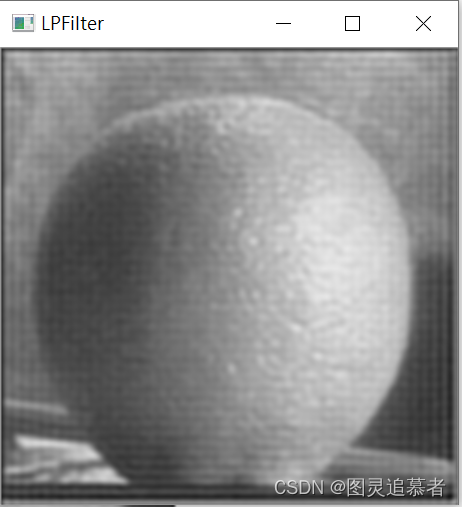
Matlab对灰度图像的频域进行高通滤波和低通滤波
1. 要求 对灰度图像进行离散傅里叶变换(Discrete Fourier Transfom, DFT)变换,在频域上分别使用理想的高通和低通滤波器进行滤波,显示滤波后的频域图像,以及逆离散傅里叶变换(Inverse Discrete Fourier Tra…
伊恩·斯图尔特《改变世界的17个方程》傅里叶变换笔记
主要是课堂的补充(yysy,我觉得课堂的教育模式真有够无聊的,PPT、写作业、考试,感受不到知识的魅力。 它告诉我们什么? 空间和时间中的任何模式都可以被看作不同频率的正弦模式的叠加。 为什么重要? 频率分量…
[EE261学习笔记] 3.傅里叶变换推导
在前几篇笔记中,我们推导了傅里叶级数相关公式,这次的笔记将进行傅里叶变换的推导 傅里叶变换的核心思想是:将任意非周期函数看作周期无限长的周期函数,因此可以调用傅里叶级数的相关公式
我们不妨设 f(t)f(t)f(t) 为周期 TTT 的…
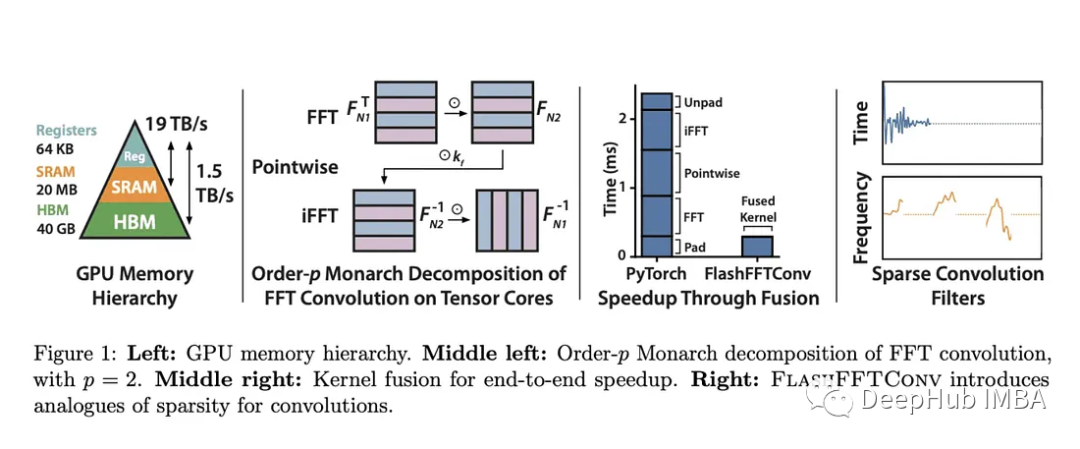
斯坦福大学引入FlashFFTConv来优化机器学习中长序列的FFT卷积
斯坦福大学的FlashFFTConv优化了扩展序列的快速傅里叶变换(FFT)卷积。该方法引入Monarch分解,在FLOP和I/O成本之间取得平衡,提高模型质量和效率。并且优于PyTorch和FlashAttention-v2。它可以处理更长的序列,并在人工智能应用程序中打开新的可…
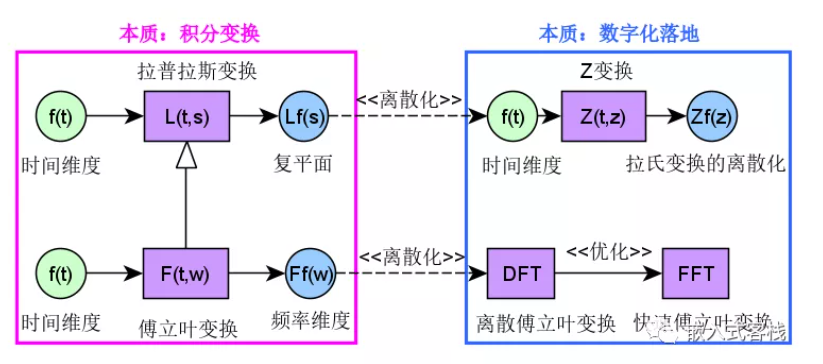
详解傅里叶变换与拉普拉斯,Z变化的联系
本文是对知乎上大佬的学习, 其知乎名为逸珺:傅里叶变换、拉普拉斯变换、Z 变换的联系是什么?为什么要进行这些变换? - 知乎
三者关系如下
如下图所示,傅里叶变换是拉普拉斯变换的特殊形式,Z变换是拉普拉斯…
数字图像处理 基于numpy库的傅里叶变换
一、傅里叶变换 图像可以用两个域表示:空间域和频域。空间域是图像最常见的表示形式,其中像素值表示图像中每个点的亮度或颜色。另一方面,频域将图像表示为不同频率和幅度的正弦波的集合。 傅里叶变换(一种图像处理中使用的数学技术)可以通过分析图像的频率分量并揭示隐藏…
个人对傅里叶分析的理解与整理(持续整理中)
一、线性空间 要搞懂傅里叶变换到底从何而来,必须要从线性空间开始。
数学中一个非常重要的概念就是空间,所谓空间其实就是将遵循一定规则的元素放在一块所形成的集合,比如研究的对象是二维的向量即满足维度为二这个规则,那么所有…
信号与线性系统翻转课堂笔记10——傅里叶变换的性质
信号与线性系统翻转课堂笔记10——傅里叶变换的性质
The Flipped Classroom10 of Signals and Linear Systems
对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著
一、要点
(1,重点&…
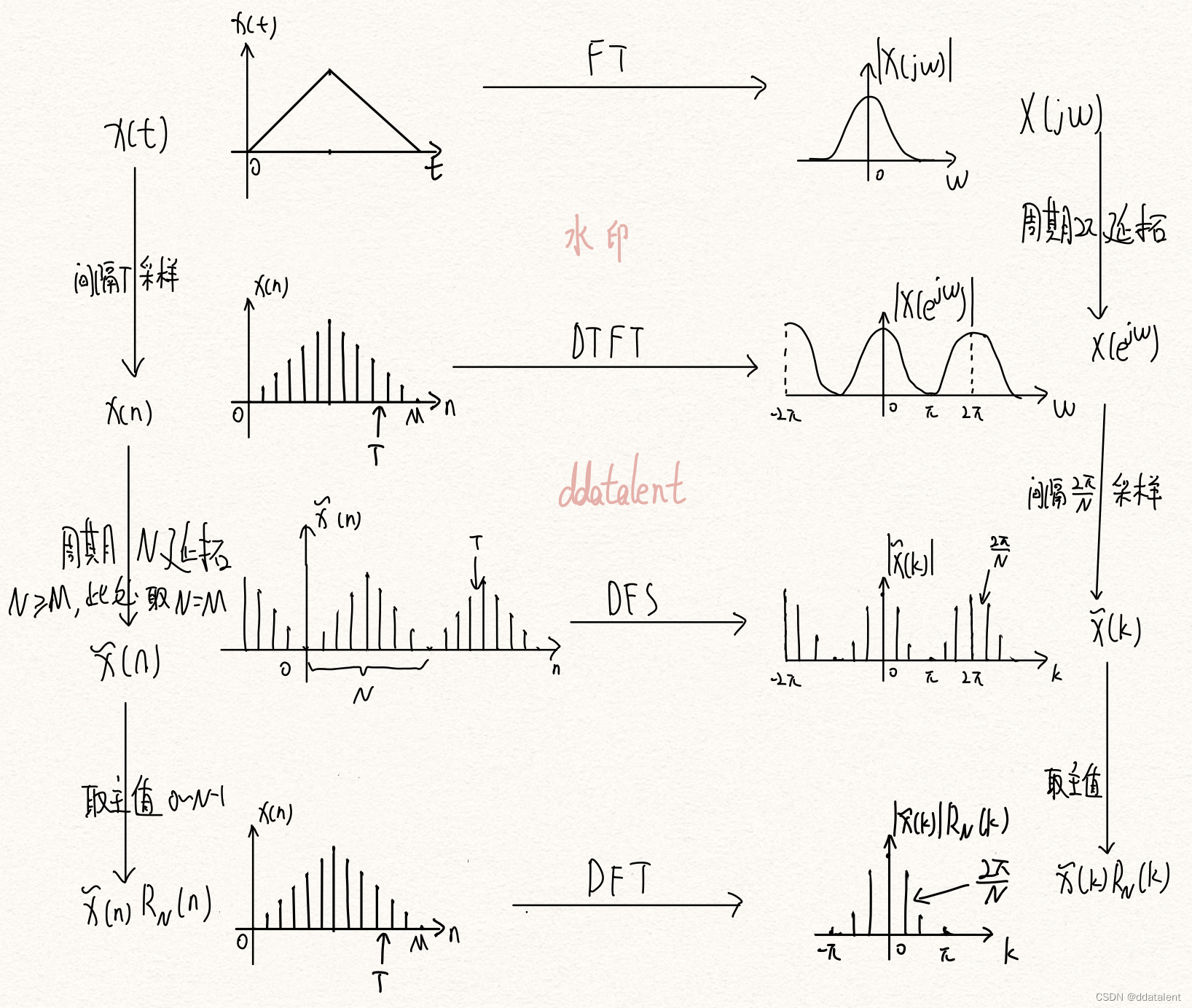
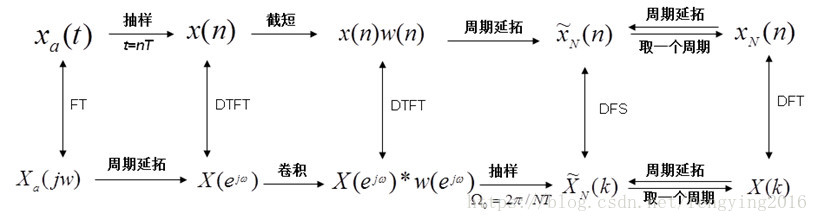
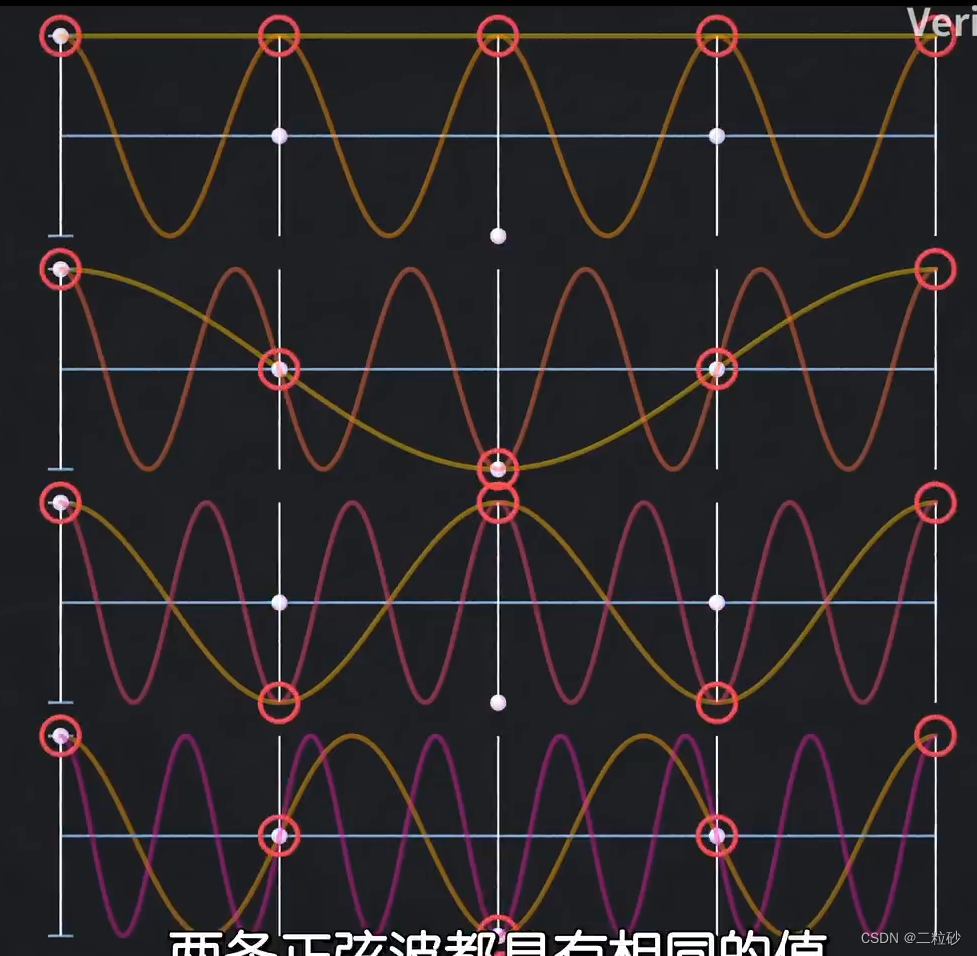
一图搞懂傅里叶变换(FT)、DTFT、DFS和DFT之间的关系
自然界中的信号都是模拟信号,计算机无法处理,因此我们会基于奈奎斯特定理对模拟信号采样得到数字信号。
但是我们发现,即便是经过采样,在时域上得到了数字信号,而在频域上还是连续信号。
因此我们可以在时域中选取N点…
【转】如果看了此文你还不懂傅里叶变换,那就过来掐死我吧【完整版】
作 者:韩 昊 知 乎:Heinrich 微 博:花生油工人 知乎专栏:与时间无关的故事 谨以此文献给大连海事大学的吴楠老师,柳晓鸣老师,王新年老师以及张晶泊老师。 转载的同学请保留上面这句话,谢谢…
![[EE261学习笔记] 3+.傅里叶变换的三个实例:矩形函数、三角函数与高斯函数](https://img-blog.csdn.net/20180516161346795#pic_center)
![[EE261学习笔记] 4.常用的几个傅里叶变换相关公式](/images/no-images.jpg)


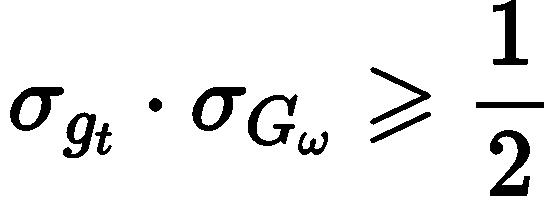
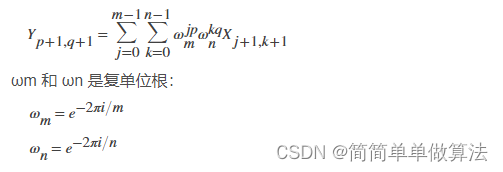

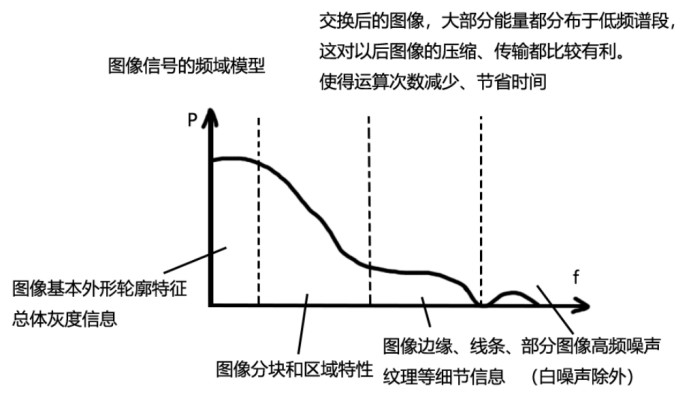

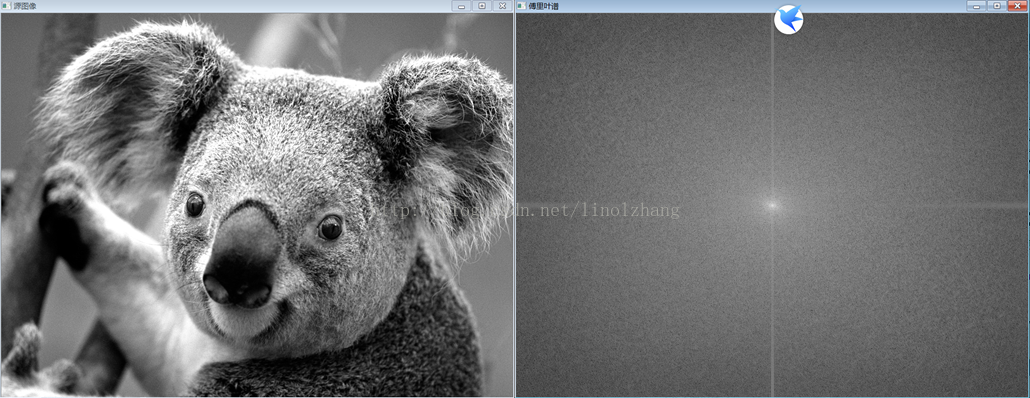

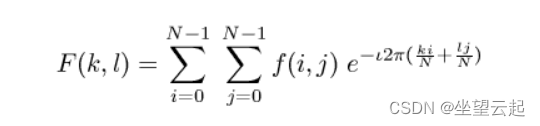

![【OFDM系列】DFT为什么能求频率幅度谱?DFT后的X[k]与x(n)幅度的关系?DFT/IDFT底层数学原理?](https://img-blog.csdnimg.cn/cf293c08cec34cc6bc7f3558efe9f039.png)
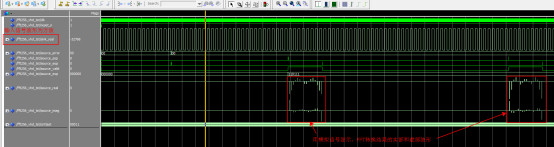






![[EE261学习笔记] 3.傅里叶变换推导](https://img-blog.csdn.net/20180511154034941#pic_center)